Hello World and FFT!

What kind of content can you expect?

I'm going to break down the content into multiple categories which you will also see in the top header: normal blog posts, tips and tricks, maybe full articles, and projects.

• Blog posts: Project updates, general news and random rants.
• Tips and tricks: A collection of hardware and software engineering tricks of the trade.
• Articles: Longer and more elaborate blog posts with a more scientific touch.
• Projects: There will be static pages for my projects with all relevant information in one place, so you don't have to dig through all the blog posts.

Let's try some math formulas and syntax highlighting

There will be many occasions on which I want to show you some piece of code or a math formula, so we need to be prepared. The syntax highlighting is done with Pygments and for math formulas I'm using MathJax (maybe with SVG image fallback in the future), which both work nicely with the Pelican static site generator. Let's see an example.

Fast Fourier Transform (FFT)

The fast Fourier transform (FFT) is a fast and efficient algorithm to calculate the discrete Fourier transform (DFT) of a digital signal. The sampled signal is divided into its frequency components, thus converting it from the time domain into the frequency domain. I will not try to explain it here any further, because there is already a vast amount of information available from other sources, but here is the formula for calculating the DFT:

$$X_k = \sum_{n=0}^{N-1}x_ne^{-j2\pi kn/N}\quad(k=0,1,\ldots,N-1)$$

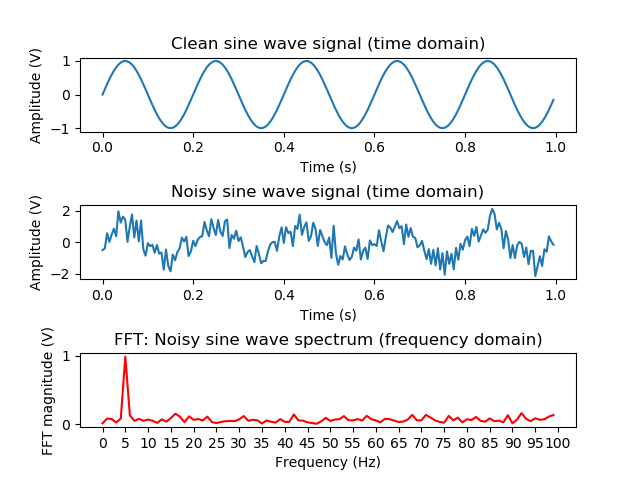
To calculate the FFT with Python we can import the NumPy package, so we don't have to implement it ourselves. The following code generates a sine wave, adds noise to it and calculates the FFT. Everything is plotted in three seperate graphs. Please note that for the visualization we display the absolute normalised (1 / N) FFT magnitude, in contrast to the above formula.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

# Copyright (c) 2018 Marco Zollinger
# Fast Fourier transform (FFT) using NumPy

import numpy as np
import matplotlib.pyplot as plt

# signal definitions
sample_rate = 200.0     # sample rate in samples/second
signal_frequency = 5.0  # signal frequency in hertz
signal_amplitude = 1.0  # signal amplitude in volt
noise_stddev = 0.5      # noise standard deviation in volt

# generate time vector 1 second long
sample_interval = 1 / sample_rate
time = np.arange(0.0, 1.0, sample_interval)
samples_count = len(time)

# generate one clean and one noisy (mean free AWGN noise) sine wave signal
signal = signal_amplitude * np.sin(2 * np.pi * signal_frequency * time)
noise = np.random.normal(0.0, noise_stddev, samples_count)
signal_noisy = signal + noise

# calculate number of frequency bins for one-sided spectrum
bin_count = int(np.ceil(samples_count / 2))
frequency_bins = np.arange(bin_count)

# calculate FFT and normalize for one-sided spectrum (except DC)
signal_spectrum = np.fft.fft(signal_noisy) / bin_count
signal_spectrum = signal_spectrum[range(bin_count)]
signal_spectrum[0] = signal_spectrum[0] / 2

# generate graphs, plot absolute of complex spectrum
figure, axis = plt.subplots(3, 1)

axis[0].plot(time, signal)
axis[0].set_title('Clean sine wave signal (time domain)')
axis[0].set_xlabel('Time (s)')
axis[0].set_ylabel('Amplitude (V)')

axis[1].plot(time, signal_noisy)
axis[1].set_title('Noisy sine wave signal (time domain)')
axis[1].set_xlabel('Time (s)')
axis[1].set_ylabel('Amplitude (V)')

axis[2].plot(frequency_bins, abs(signal_spectrum), 'r')
axis[2].set_title('FFT: Noisy sine wave spectrum (frequency domain)')
axis[2].set_xlabel('Frequency (Hz)')
axis[2].set_ylabel('FFT magnitude (V)')

plt.xticks(np.arange(0, 105, 5))
plt.subplots_adjust(hspace=1.0)
plt.show()

Example output. The peak in the FFT magnitude for the frequency of the input signal is clearly visible despite the noise:

Written by Marco Zollinger in blog on Thu 10 May 2018. Tags: FFT,